The current Earendil routing system is based on purely source routing + onion routing: the sender of a packet plots the full path to the destination using the relay graph, and sends an packet along the path, onion-encrypted with the public keys of every relay along the way. Each relay then peels off one layer and forwards it to the next hop:
The problem with this approach is that performance and anonymity depends on the specific shape of the Earendil network. This can be pretty bad news.
For performance, the downside is obvious: if a client wants to talk to a relay that is 10 hops away, it must process 10 layers of onion encryption even though that might be entirely superfluous for anonymity.
How this coupling damages anonymity is a little more subtle. On one hand, there’s an old paper by George Danezis that shows that mix networks with similar topologies — where the “next hop” of each hop is restricted to a few neighbors — actually do achieve reasonably good anonymity given pretty loose assumptions on the shape of the network.
Unfortunately, it’s hard to assume things about what Earendil’s relay graph will look like. The “friend-to-friend” design suggests a social graph, about which there’s quite a bit of data and research, but there are many plausible scenarios in which node connections in Earendil would not follow real-life social relationships. For instance, the network might be largely hub-and-spoke, dominated by professional relay operators each with thousands of connections to smaller nodes, but who only connect to each other sparsely. Such a graph might not even have many long paths. In these cases, the anonymity guarantees given by the paper would no longer apply.
Fortunately, both of these problems can be fixed by decoupling onion-peeling from routing.
A brief description of the new algorithm
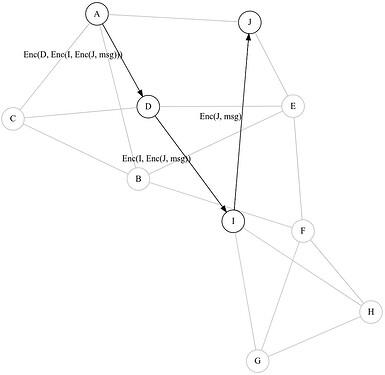
When a node N wishes to talk to a relay R, instead of finding some path through the network that starts with a neighbor of N and ends at R, it arbitrarily picks k nodes N1, … Nk. It then onion-encrypts the message with the public keys of N1, … Nk, R and then sends the message to the neighbor on the shortest path to N1.
When a node receives an incoming message, it looks at the outermost layer of onion encryption to see whether it can decrypt the message. If not, it is forwarded, verbatim, to a neighbor one hop closer to the node with the public key written on the outermost layer of encryption. Which neighbor is closer is always possible to tell, since we have the entire relay graph.
If the message can be successfully peeled, the next layer is sent to the neighbor on the shortest path to the the node who can decrypt the next layer.
The message eventually takes some path and finds itself at N1, who peels one layer of encryption off, then takes some other path to find itself at N2, etc, until it arrives at R correctly.
The important part here is that we no longer fully source-route the entire path from N to R. Instead, packets on the way to the intermediate “peelers” are routed hop-by-hop like on the Internet.
The whole system now greatly resembles overlaying a mixnet on top of an Internet-like, non-anonymous system.
Why is this better?
For performance, a person wishing to trade off all anonymity for speed can now avoid picking any intermediate peelers and directly send a message addressed to R. Things do not get faster than that.
For anonymity, we can have every user sample the intermediate peelers from the same distribution, regardless of where they are in the route topology. This increases the anonymity set, and the anonymity will increase with the number of relays in the network regardless of the shape of the topology. We could have a network where every single relay connects to the same massive hub and still have the same anonymity as a spread-out mesh network.
A small hurdle with incentives
An overlay network like this might make incentives harder — peeling a message is more expensive than merely forwarding it verbatim. Consider a message that travels through the following path, where the relays in bold are peelers and the rest are not:
A → B → C → D
C will incur more costs than the other nodes.
If we use our usual approach of hop-by-hop payments, this means that C would want to charge B more than the rate that it would charge B if the packet were not to be peeled by C. But in that case, B would lose money on this packet unless it upcharges A — and A has to upcharge the sender.
But due to onion encryption, A doesn’t even know that there’s a “peeling” action down the line, so how can it charge the right price? Fixing this seems to require breaking onion encryption, ruining anonymity.
What if the sender pays the first peeler out of band, who then pays the second peeler, etc? Unfortunately, this can also lead to deanonymization, since this way, the payment graph (who pays whom) will actually leak information about the communication graph (who is talking to whom), while in the hop-to-hop payment case it does not leak information beyond the relay graph (who is neighbors with whom), which is already public.
Instead, we must ensure that forwarding costs are dominated by bandwidth rather than peeling. This will make this whole problem moot. Fortunately, we are already most of the way there, given Earendil’s large packet sizes (which reduces per-bytes peeling cost) and heavy link obfuscation (which increases bandwidth costs).
Implementing the new approach
We plan on implementing this new approach in the same update that will contain a basic mix network implementation (Poisson delays, etc).