The Melmint v2 documentation gives a fairly detailed explanation of the core Melmint mechanism. In short:
- Minters produce ERG at a cost of k ERG / 1 DOSC and likely exchange the ERG for “useful” tokens on-chain.
- ERG/SYM exchange rate in Melswap then defines “1 DOSC worth of SYM”
- Magic printed money then continually nudges SYM/MEL swap pool to be closer to 1 MEL = 1 DOSC worth of SYM
- Combined with arbitrage, this makes 1 MEL’s market price converge to 1 DOSC.
However, in my experience there are a few subtle points in Melmint that often cause misunderstandings and deserve some more exploration, so here are some somewhat unorganized thoughts on them.
The role of liquidity
TL;DR: Melmint “peg strength” relies on SYM/MEL liquidity. But other pools’ liquidity does not really matter — as long as there’s enough liquidity to make sustained mispricing impossible. That liquidity is actually much smaller than the liquidity needed to resist short-term market manipulation.
Melmint v2 depends heavily on the built-in Melswap DEX. This naturally raises the question of whether liquidity issues on Melswap might cause instability, since a lack of liquidity can cause price feeds to become inacccurate or easy to manipulate.
The answer is different for the two pools that Melswap reference: SYM/MEL and SYM/ERG.
SYM/MEL liquidity = Melmint strength
On one hand, liquidity in the SYM/MEL pool is very important: to hold the “1 MEL = 1 DOSC worth of SYM” peg, Melmint prints new MEL or SYM in proportion to liquidity already in the pool. This means that without liquidity in the pool, Melmint will simply turn off. Note, however, that this is intentional to avoid death spirals — market expectation of a death spiral will lead to a massive decrease in SYM/MEL liquidity as people liquidate both assets, turning off Melmint and preventing a death spiral (this explored further in the Melmint docs). But in normal circumstances, there should be plenty of on-chain liquidity since SYM and MEL are the biggest two on-chain assets, and the Melmint stabilization mechanism essentially subsidizes liquidity provision by artificially generating fee-producing activity.
SYM/ERG liquidity is not that important
On the other hand, the SYM/ERG pool is only used as a price feed to determine “1 DOSC worth of SYM”. Therefore, all it needs is to have enough liquidity an accurate exchange rate; any more liquidity beyond that does not really matter.
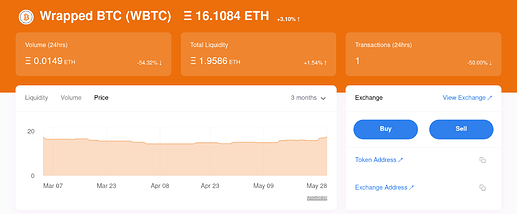
And thanks to the power of arbitrage, the amount of liquidity needed for accurate prices is surprisingly small! Let’s look at Uniswap v1 — a doubly-obsolete DEX with little liquidity left. For instance, right now the ETH/WBTC pool has a pathetic 1.95 ETH of liquidity:
Yet the exchange rate, 16.1084 ETH = 1 WBTC, is only 0.3% away from CoinGecko’s exchange rate:
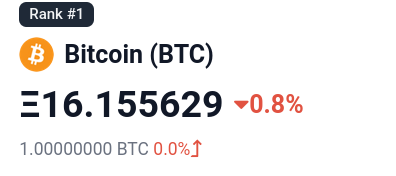
This pattern holds true for many other thinly-traded tokens: because arbitrageurs can profit from price deviations even in AMM pools with little liquidity, prices tend to be accurate.
What about manipulation?
But wait! Thinly traded pools like the Uniswap v1 seem very easy to manipulate: anybody can spend a few ETH to double the price of WBTC! Indeed, something like a lending protocol using Uniswap v1’s WBTC/ETH exchange rate would be a horrible idea, since wrong exchange rates even in the short term can cause catastrophic results.
Long-term market manipulation, on the other hand, is extremely difficult. When an attacker holds the price at a level different from the prevailing market price, arbitrageurs are incentivized to “correct” the price at the expense of the attacker. For example, if I double the price of WBTC on Uniswap v1, then everybody else would be incentivized to buy WBTC elsewhere and sell it on Uniswap v1, using the ETH gained to buy more WBTC elsewhere, ad infinitum. This will push the price back to normal, unless I throw in even more ETH to move the price back up.
To succeed in the long run, I must therefore be prepared to buy an unlimited amount of WBTC at twice the market price. This dooms me to outspend the rest of the world!
Market prices being correct is thus a classic case of endogenous trust: due to the incentives involved, we only need a rational majority assumption, not an honest majority assumption, since attackers must overpower not just all honest players, but all profit-motivated ones. Moreover, this has nothing to do with how much liquidity is in the pool: whether there’s 1, 10, or 1000 ETH of liquidity only affects how easy it is to initially shift the price, not hold it there long-term.
Fortunately, Melmint cares far more about the long-term correctness of Melswap prices than short-term accuracy, since it only slightly “nudges” the MEL/SYM exchange rate at the end and is intend to operate on noisy data. So it’s very unlikely that Melswap prices can be manipulated to such an extent that Melmint is significantly destabilized, even though the ERG/SYM pool would probably have much less liquidity than the MEL/SYM pool due to the small supply and demand of ERG.
(One exception is if the market is so extremely illiquid that transaction fees make it impractical for anybody to exploit the arbitrage opportunity. But that’s very unlikely even for the ERG/SYM pool)
The market for ERG
TL;DR: initially, ERG demand is subsidized slightly by the block reward, but eventually the subsidy goes to zero. Fortunately, Melmint doesn’t actually require too much demand for ERG; just some small nonzero demand. so the absence of the subsidy will not cause issues. This is because the supply for ERG is extremely elastic.
Melmint’s central “oracle” is the SYM/ERG exchange rate, which tries to measure the value of a SYM in terms of DOSC. In particular, k ERG is supposed to be equivalent to 1 DOSC, where k is the number of ERG that can be produced with 1 DOSC of sequential CPU work.
As specified in TIP-909a, a small portion of SYM inflation goes to buy and burn ERG from the SYM/ERG pool. While SYM is still inflating, this acts as a continual auction of freshly printed SYM for freshly burnt ERG; it’s fairly clear that this establishes a market price for SYM in terms of DOSC.
What is more subtle is when SYM inflation eventually runs out. Without the subsidy, ERG demand will probably greatly decrease, since ERG is (intentionally) quite useless as a token. Most ERG would be immediately dumped by minters, and its demand will probably come from marginal usecases, such as as an intermediary asset in arbitrage, “day-trading” minters holding on to their ERG for a while to sell at what they think will be a higher price, etc. Will this be sufficient to drive Melmint?
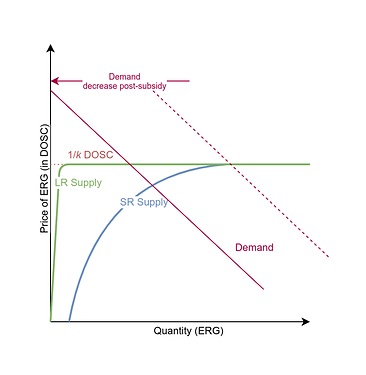
The answer is fortunately yes: as long as there’s some nonzero demand for ERG, k ERG will closely track its minting cost of 1 DOSC. This is because ERG is designed to have close to perfectly elastic supply. This means that an unlimited amount of ERG is “for sale” at prices above the 1/k DOSC minting cost, while close to zero is “for sale” at prices below the minting cost. With almost any demand curve, this leads to the equilibrium price being k ERG = 1 DOSC, as illustrated in this demand/supply graph:
How does ERG have such an elastic supply? There are two important pieces:
- First, because 1 DOSC of work produces a guaranteed k ERG, ERG always has perfect supply elasticity at prices above the 1/k DOSC target. This is because an unlimited amount of minters can then profit by minting an ERG for 1/k DOSC worth of CPU costs and then selling the ERG for this higher price. Thus, an unbounded amount of ERG will dump onto the market until the price is at or below 1/k DOSC.
- Second, because k rapidly increases over time, long-run supply of ERG is close to perfectly elastic even at lower prices, even though short-run supply might not be. In the short run (“SR supply in the graph”), when the ERG price is below the minting cost of 1/k DOSC, supply does not immediately drop to zero, since even though it’s no longer profitable to mint any more ERG, old ERG might still be trading in the market at a discount. But because of the increasing value of k, it’s as if these ERG gradually get destroyed — it might help to think of “kERG” as the currency, and the k increase as a steep demurrage. This destroys the “old ERG stash”, making the supply when the price is lower than 1/k DOSC quickly converge to zero.
In conclusion, due to the extremely elastic supply of ERG, even drastic fluctuations in a tiny ERG demand should not cause significant changes in the ERG price, making the ERG/SYM price feed a reliable anchor for driving Melmint.
DOSC stability
TL;DR: the real value of DOSC will of course vary, but there are some interesting heuristic arguments that both long-term and short-term stability is likely to be better than a commodity-based peg.
The final objective of Melmint is to peg 1 MEL = 1 DOSC, but this is only meaningful if DOSC actually has a stable purchasing power. But why would that be the case?
Of course, there’s historical data that suggests DOSC stability, but I would argue that the strongest arguments for DOSC stability are actually a priori rather than empirical, since it’s difficult to accurately gauge past DOSC values without any markets that incentivize DOSC price discovery. Thus I’ll give a brief a priori argument here on why a DOSC peg should have better price stability than a peg to some natural scarce commodity, since a commodity peg is the “usual” historical form of non-fiat currency (gold standard, silver standard, Rai stones, etc).
Long-term stability
Let’s start with long-term stability, since that is one area where fiat currency fails terribly and non-fiat alternatives are most pressing. We immediately run into a problem — it’s difficult to precisely define “real value” over long periods of time since patterns of consumption etc can change dramatically over time. We certainly cannot measure value in terms of money (that’d be “nominal value”), since money’s value itself can rise and fall! So let’s use a first approximation — the “real value” of some good is simply the fraction of resources in the whole economy consumed in pursuit of that good. This essentially pins down the vague notion of the exchange rate of that good “measured against everything else”; the consumer goods baskets used for calculating CPI are also approximations of the same idea.
In this perspective, then, it’s actually not clear that most commodity standards have long-term stability, since natural commodities do not scale with technological changes. For example, the real value of one gram of gold in the year 2100 — what fraction of the rest of the 2100 global economy can you buy with it — will be extremely different in the following two worlds:
- A world where asteroid mining makes gold a common metal and 1 gram of gold is thus extremely “cheap”.
- A world where gold is just as scarce as right now, but it turns out the only way to travel to other star systems is by building interstellar portals made out of solid gold. A far greater fraction of the economy (all interstellar trade!) then counts on the very limited amount of gold we have, thus making 1 gram of gold extremely “expensive”.
On the other hand, sequential computation time scales with most technological changes. This is because computation as a fraction of total economic value will stay relatively constant as long as we are a society where computers play a relatively constant role. Taking a constant, Nature-defined piece of this relatively constant fraction, rather than anything that can be improved technologically (e.g. 1000 hashes), then gives us a relatively constant real value.
Of course, the fraction of the economy that computation is worth may change, since our society as a whole could become more or less computation-intensive. On one hand, we might all be living in a virtual metaverse, consuming oodles of e.g. physics computation for basic tasks like “walking” down a “street”. On one hand, something like asteroid mining might drastically boost the importance of another economic sector (in this case, mining), squeezing the share taken up by computation.
But generally speaking, the production structure of an economy (what kinds of goods take up what fraction) changes much more slowly than productivity (how “good” and how abundant the goods are). DOSC value is affected by the former, while commodity value changes with the latter.
Short-term stability
It’s easier to see DOSC’s superior stability to commodities in the short term. Unlike commodities commonly used to back currencies like gold or silver, sequential computation time is produced using greatly diversified factors of production:
- Natural resources to build the CPUs (silicon, gold, etc)
- Different natural resources to generate energy to run the CPUs (fossil fuels, nuclear fuel, etc)
- Human labor in CPU factories
- Technology / intellectual property in CPU design
- etc
This diversification tends to dampen the effect of individual shocks (say, a sudden gold shortage) on the final price of computation. Furthermore, since CPU production firms tend to have many costs that are very sticky, like wages, office rentals, and debt repayments, they are strongly incentivized to sell their products at a short-term fixed price to smooth out their income and reduce risk.
On the other hand, essentially all the value of a commodity comes from one factor: “economic land”, or basically value that already comes in nature, rather than from labor or capital investment. Not only does this mean a lack of diversification, it also means that unlike the CPU production business, the commodity mining and trading business is very “lean”, dominated by highly liquid and volatile resource prices and minimally dampened by the usual “sticky prices” of things like wages and rent.